Menu
Regular Polygon Calculator
Use this advanced math calculator to calculate the properties of a polygon. Simply enter any known value of a polygon to calculate the missing properties of a polygon, entering the number of sides and length of a polygon side will calculate all other properties of a polygon, alternatively you can enter the interior/exterior angle or any of the other known properties to complete all associated polygon calculations. When you enter the number of sides present on the polygon and the Advanced Polygon Calculator will tell you the name of the polygon, for example, a 12 sided shape is a Dodecagon.
| The Polygon name for a sided shape is a |
| The length of the sides (l) of the is |
| The Interior angle (∠x) of the is ° |
| The Exterior angle (∠y) of the is ° |
| The Circumradius (R) of the is |
| The Inradius (r) of the is |
| The Area (a) of the is 2 |
| The Perimeter (P) of the is |
| The length of the sides (l) of a formula and calculations |
|---|
| l = P/n l = / l = |
| The Interior angle (∠x) of a formula and calculations |
| ∠x = 180 - 360/n ∠x = 180 - 360/ ∠x = |
| The Exterior angle (∠y) of a formula and calculations |
| ∠y = 360/n ∠y = 360/ ∠y = |
| The Circumradius (R) of a formula and calculations |
| R = l/ 2 × sin(π/n) R = l ÷ 2/sin(r) R = ÷ 2/sin() R = ÷ 2/ R = |
| The Perimeter (P) of a formula and calculations |
| P = n × l P = × P = |
Please rate this calculator
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
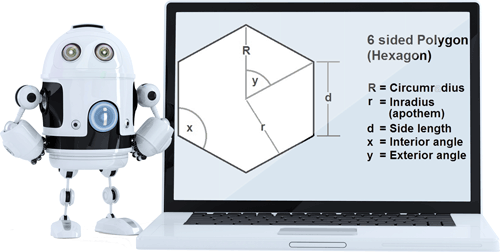
About the Regular Polygon Calculator?
Mathematical calculations stop being easy after a certain point, and rightly so. After all, complex problems can only be solved using an elaborate calculation. Thus, making advanced polygon calculations a tough nut to crack. This is where the Regular Polygon calculator saves the day. Let's take a look at what all functions the Regular Polygon calculator performs.
Functions of Regular Polygon Calculator
The Regular Polygon calculator developed by iCalculator simply requires you to type in the following data:
- Number of sides (minimum number being 3)
- Length of sides
- Choose the units (mm, cm, metres, inches, feet and yard)
And that's it, the calculator automatically gives you the following information about the polygon:
Interior Angle (x)
The interior angle of a polygon is the angle made by two adjacent sides. The formula for calculating the sum of all interior angles is (n-2) x 180°, where 'n' is the number of sides. Divide the product of the formula above with the 'n' itself, and you'll have the measurement of one interior angle.Note that the amount entered must be less than 180.
Exterior Angle (y)
An exterior angle is the angle made when one of the sides are extended on its plane towards the outside plane. Naturally, the exterior angle will the difference between the linear angle (180°) and the interior angle.
For example; the interior angle of an equilateral triangle is 60°. So, the exterior angle will be 180° - 60° = 120°. Unit is degrees (If either of the angles are changed then the nearest number of sides will be used and angles adjusted)
Circumradius (R)
In geometry, a circle drawn such that touches all the vertices of a cyclic polygon is known as a circumcircle. The radius of such a circle is known as circumradius.
Let the polygon in question be a triangle with sides a, b and c. The circumradius of a circle drawn will be:
Alternatively, you can also use the following formula to find the length of the circumradius
Where 'S' is the length of the side of the polygon.
Inradius (r)
Considering the same triangle from the example above, draw three dotted;ines from each vertex that divide and angles into half towards the center of the triangle. The point where these three lines intersect is the incenter, and the circle thus drawn will be the incircle. From the center, draw a line that is perpendicular to any of the sides. This perpendicular line is the inradius.
The formula for calculating the inradius of a triangle with sides a, b and c is:
Where s is the semiperimeter of the triangle which is further calculated by the following formula:
Area of the Polygon
To find the area of a polygon, you need to know the terms apothem (a) and perimeter. Apothem is a line that starts from the center of the polygon and is a perpendicular bisector of any side. Perimeter is the sum total of all the sides.
With this information in mind, the perimeter of the polygon can be calculated by the following formula:
Why Use the Regular Polygon Calculator
The key reason behind using an advanced polygon calculator is to find all the above attributes of a polygon in the quickest and easiest way. Instead of calculating all of the above one by one, you get all the results instantly and simultaneously.
Conclusion
Modern times call for more math functionality and the quick application of formulas instead of spending time on math calculations. While a simple calculator can also give you the desired results, it will take significantly more time than using our state-of-the-art regular polygon calculator.