Math Lesson 9.8.2 - Systems of Equations with One Linear and One Quadratic Equation

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Math lesson on Systems of Equations with One Linear and One Quadratic Equation, this is the second lesson of our suite of math lessons covering the topic of Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

Systems of Equations with One Linear and One Quadratic Equation

So far, we have dealt only with linear equations when solving systems. However, not all systems of equations are linear. Very often you may face situations in which one or both equations in the system are not linear. In this paragraph, we will explain how to solve systems of equations with one linear and one quadratic equation. We can distinguish the following cases:

1. Only one variable is to the second power in the quadratic equation

This is the simplest case of the linear - quadratic combination in the systems of equations. Let's use an example to clarify this point. For instance, let's consider the following system of equations:

As you see, only the variable x is raised to the second power in the quadratic equation. Such systems are better solved with the substitution method. We can either express y in the first equation in terms of x, i.e.

and substitute it in the quadratic equation, or maybe express x in terms of y in the same equation, i.e.

and eventually replace x in the quadratic equation with the above expression. Let's choose the latter substitution to avoid fractions. Thus,

We have a = 9, b = 7 and c = -16. The discriminant Δ is

Thus,

and

Each y-variable has an x-variable in correspondence. We can use the linear equation to find x, as it allows an easier solution. Thus, since

we have for y₁ = -16/9:

and for y₂ = 1:

Therefore, we have two pairs of coordinates as solution sets for this system of equations. Each pair represents a point in the coordinate system where the graphs of the two equations intercept. These points are A(x¹, y¹) and B(x², y²), or more specifically, A( - 39/9, - 16/9) and B(4, 1).

The graphical solution of this system of equations is shown below.

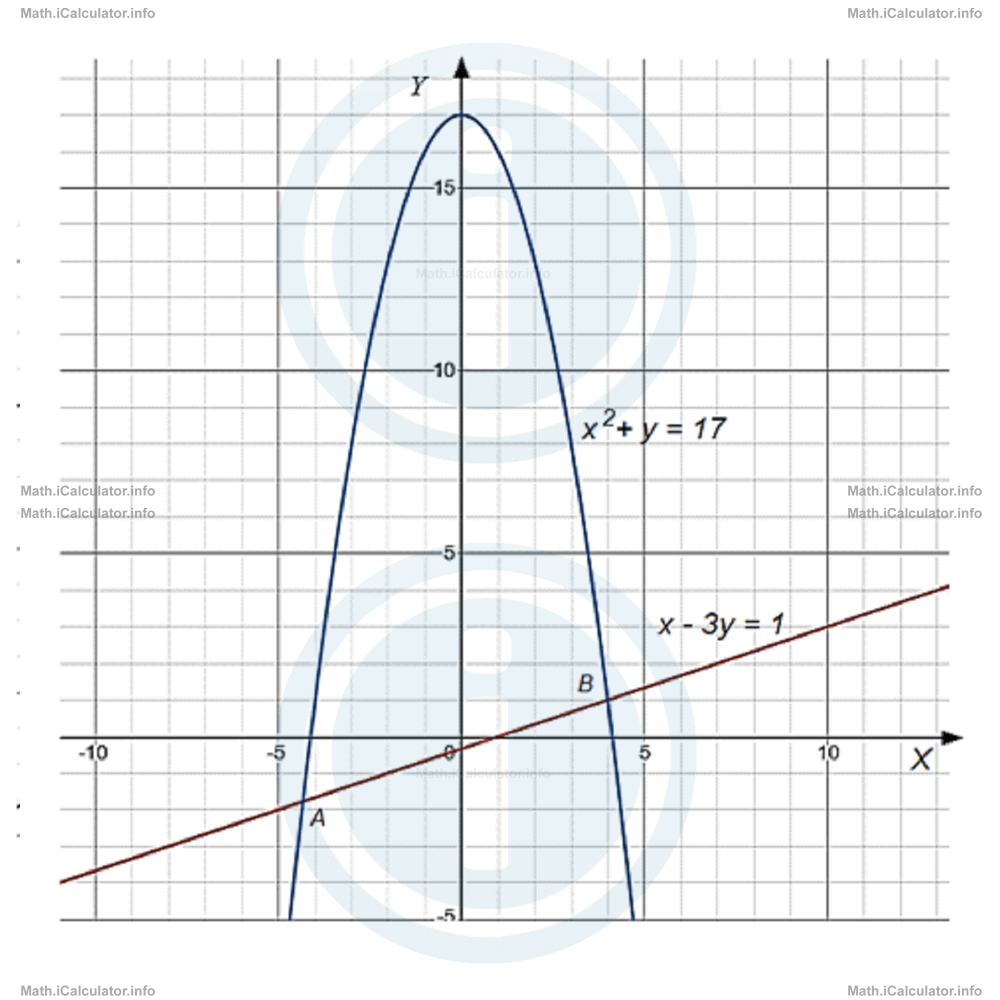
Here too, we can determine the type of relationship between equations graphs in the system based on the number of points they have in common. Thus,

1. When the two equations have two points in common (two pairs of solutions), like the system in the above example, the graphs are said to be intersecting.
2. When the two graphs have a single point in common (one pair of solutions), the graphs are said to be tangent.
3. When the two graphs have no points in common (no solutions), the graphs are said to be divergent. The system of equations in this case is inconsistent.

Example 2

Without plotting the graphs, determine the number of points the equation graphs in the systems below have in common. After solving each system, then check the solutions graphically.

1. x - y = 1x² - 2y = 1
2. 2x + y = 7x² - y = - 9
3. x - 3y = 2x + y² = 6

Solution 2

1. We can replace y with x - 1 in the second equation. This replacement is obtained by expressing y in terms of x in the first equation. Thus, we obtain
   x² - 2 ∙ (x - 1) = 1
   x² - 2x + 2 = 1
   x² - 2x + 2 - 1 = 0
   x² - 2x + 1 = 0
   This quadratic equation belongs to the family of the second algebraic identity, which can be factorised as (x - 1)². It has a single solution, x = 1.
   You can also reach this conclusion by proving that the determinant is zero, i.e.
   ∆ = b² - 4ac
   = ( - 2)² - 4 ∙ 1 ∙ 1
   = 4 - 4
   = 0
   Hence,
   x = - B/2a
   = -(-2)/2 ∙ 1
   = 2/2
   = 1
   Since there is a single x as a solution, there will be a single y as well. Substituting the value found for x in the first equation (for convenience), yields
   1 - y = 1
   y = 1 - 1
   y = 0
   Therefore, the point A(1, 0) is the only point of convergence between the graphs. This means they are tangent.
   The following figure shows the graphs of both equations of the first system.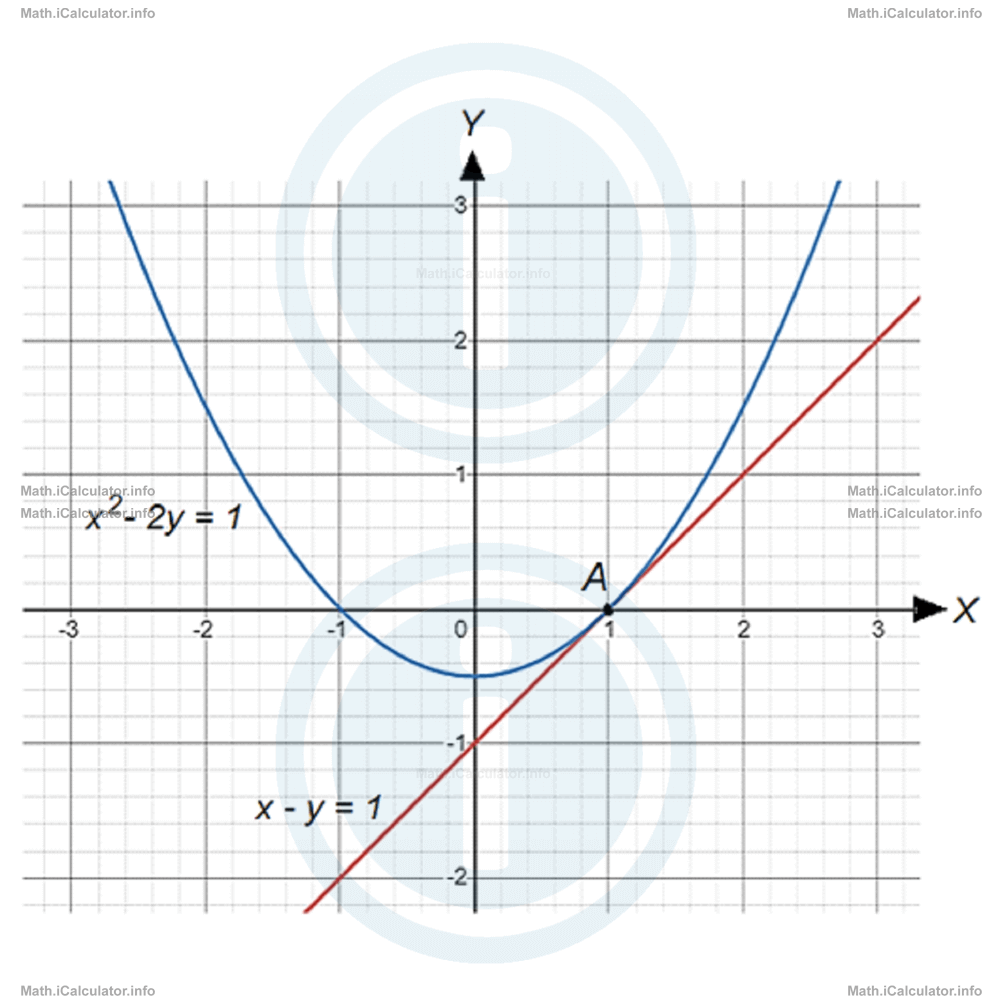
2. We can try solving this system of equations through the elimination method, as this is more convenient. Thus, adding the two equations of the system to eliminate y, yields
   2x + y = 7x² - y = - 9
   x² = - 2
   The last equation has no solution, as there is no number that gives - 2 when raised to the second power. Therefore, the system of equations is inconsistent, and the graphs of the corresponding equations have no common points, as you can see in the figure below.
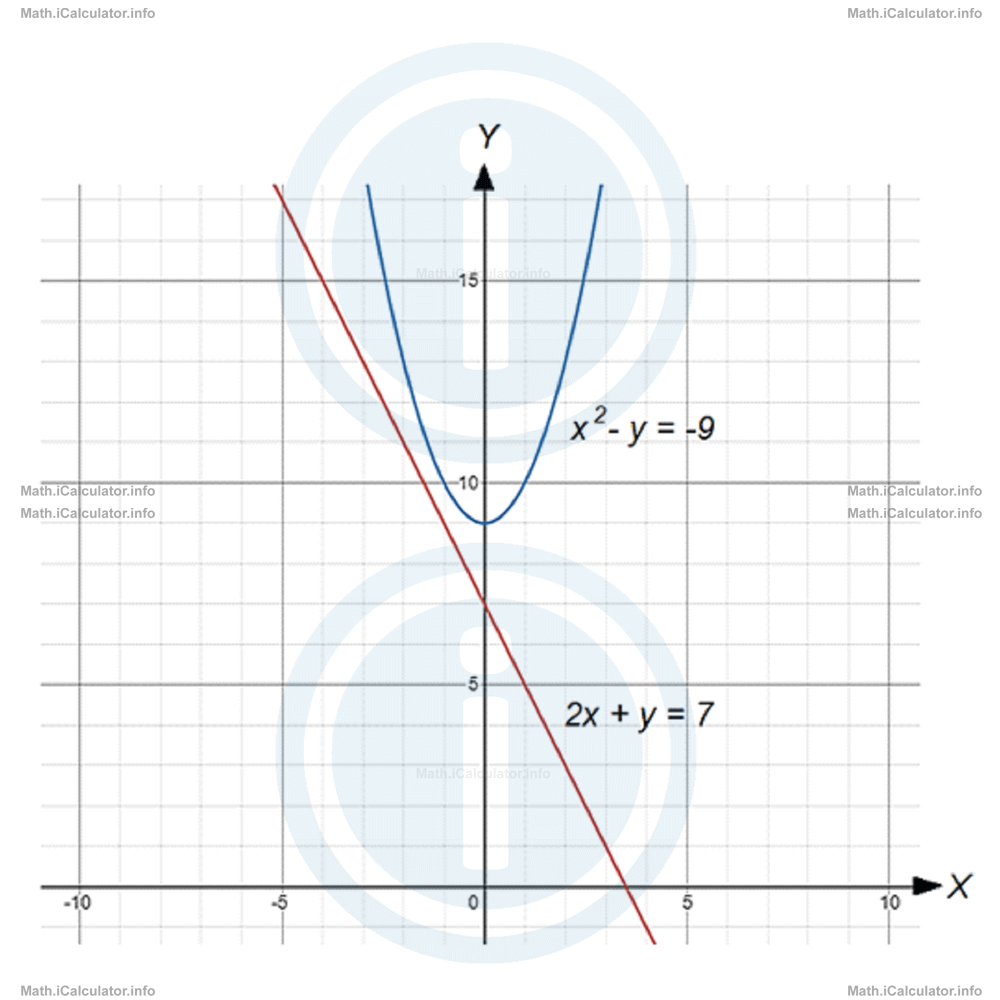
3. This time, it is the variable y raised in the second power in the quadratic equation, but this is not important. Again, it is better to solve this system by elimination method after multiplying by - 1 the first equation of the system. Thus,
   x - 3y = 2x + y² = 6
   - x + 3y = - 2x + y² = 6
   Adding the two equations to eliminate x yields
   y² + 3y = - 2 + 6
   y² + 3y = 4
   y² + 3y - 4 = 0
   In this quadratic equation we have a = 1, b = 3 and c = -4. Thus, the discriminant Δ is
   ∆ = b² - 4ac
   = 3² - 4 ∙ 1 ∙ ( - 4)
   = 9 + 16
   = 25
   From here, we obtain
   y₁ = -b - √∆/2a
   = -3 - √25/2 ∙ 1
   = -3 - 5/2
   = -8/2
   = - 4
   and
   y₂ = -b - √∆/2a
   = -3 + √25/2 ∙ 1
   = -3 + 5/2
   = 2/2
   = 1
   Hence, the graphs of the two equations of the system are intersecting, as they have two points in common. Let's find the two corresponding x-coordinates of the intersections. We have
   x₁ - 3 ∙ 4 = 2
   x₁ - 12 = 2
   x₁ = - 10
   and
   x₂ - 3 ∙ 1 = 2
   x₂ - 3 = 2
   x₂ = 5
   Therefore, points A( - 10, - 4) and B(5, 1) are the intercepts of the graphs. (We always take as point A the one that is more on the left, regardless of whether it is the first solution or the second).
   The figure below shows the two graphs including the intersection points A and B.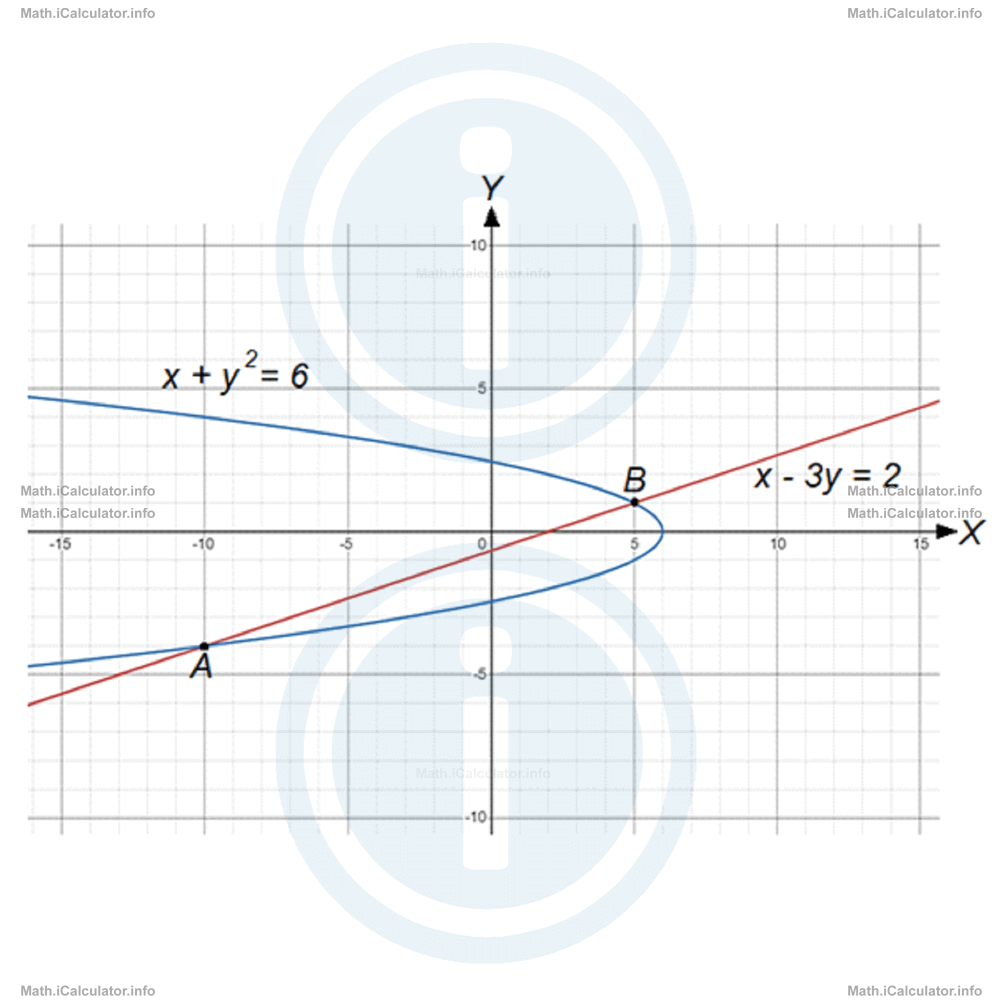

2. Both Equations are Quadratic

If both equations in a system are quadratic, we may have zero to three pairs of numbers as a solution set. The only difference in the procedure of solutions with the systems discussed in the previous paragraph - where one of the equations was linear and the other quadratic - consists of the fact that now we have to substitute the square of a given variable instead of a variable in the first power. Then, the rest of the procedure is the same.

Let's clarify this point through an example. Consider the following system of quadratic equations:

We can solve this system with any of the first two methods. Let's use the substitution method. Thus, from the first equation, we obtain y in terms of x and then, we substitute it in the second equation. We have

Thus, in the equation

we write

Thus, we have two roots for this quadratic equation: x¹ = -1 and x² = 1. These values are also intercepting points of the two graphs. Let's find the corresponding y-coordinates, as they represent the other two solutions of the system. Thus, for x¹ = -1, we have

and for x² = 1, we have

Despite the fact we got the same values twice for y, they represent different points, as the x-coordinates are different. We have two intercepts, therefore: A(-1, -4) and B(1, -4). Look at the figure below, where the two graphs of the system's equations are shown.

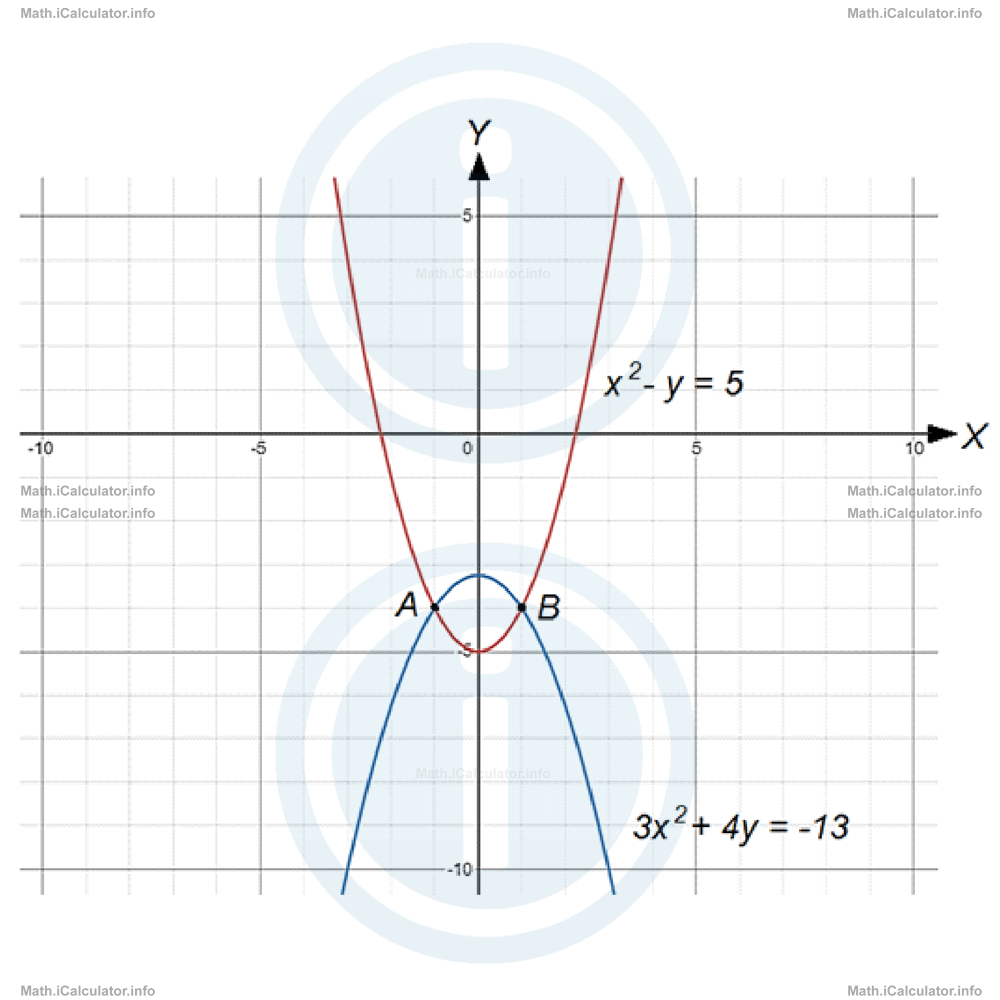
Example 3

Find the type of relationship between the graphs of the equations contained in the following systems. Then check your solution applying the graph method.

1. x² - y = -13x² + 2y = - 7
2. x² + 2y = 0x - y² = 0

Solution 3

1. We can express y in terms of x with the help of the first equation and eventually substitute in the second equation the expression obtained. Thus,
   x² - y = -13x² + 2y = -7
   y = x² + 1
   so,
   3x² + 2 ∙ (x² + 1) = -7
   3x² + 2x² + 2 = -7
   5x² = -9
   x² = -9/5
   = -1.8
   This equation has no solution in the set of real numbers, as no real number can multiply by itself and give a negative number as a product. Therefore, the two equations in the system are inconsistent and the corresponding graphs do not have any meeting or intersection point, as you can see in the figure below.
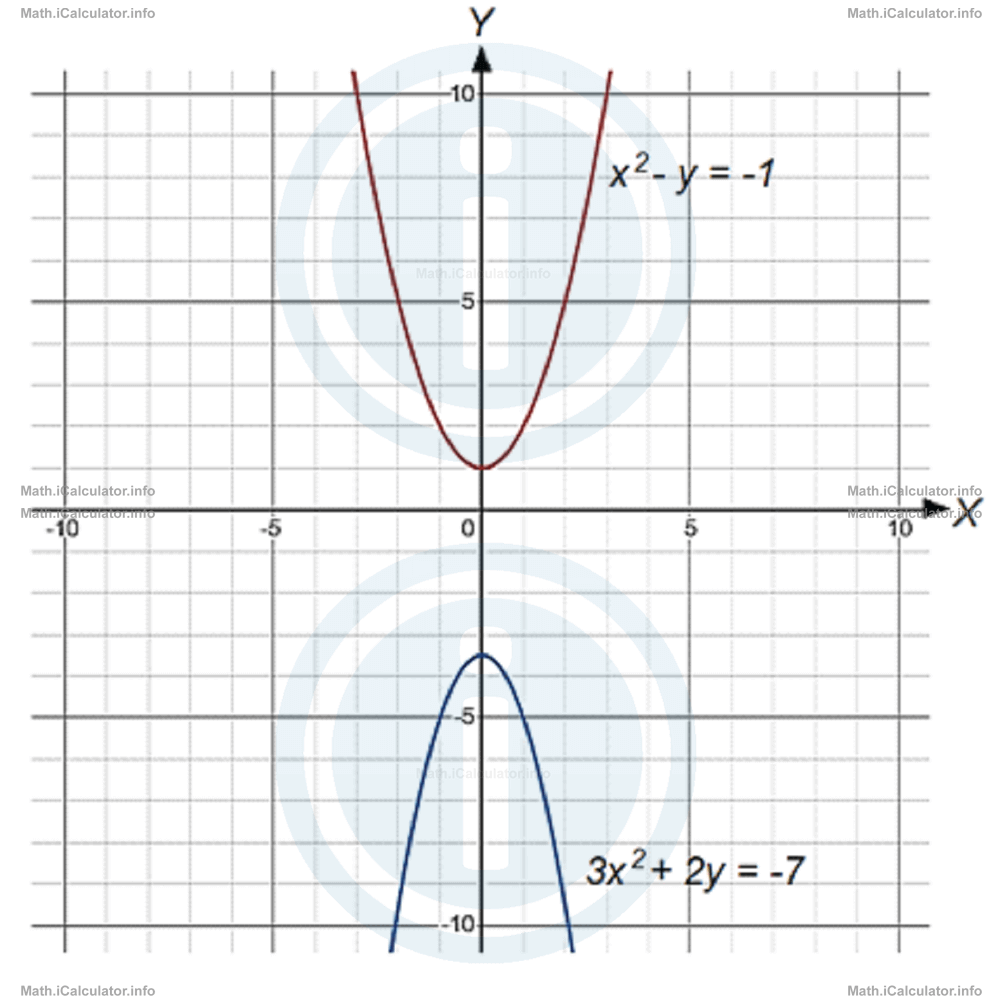
2. We can express x in terms of y with the help of the second equation and eventually substitute in the first equation the expression obtained. Thus,
   x² + 2y = 0x - y² = 0
   x = y²
   so,
   (y² )² + 2y = 0
   y⁴ + 2y = 0
   y(y³ + 2) = 0
   This equation is true for y = 0 and y³ + 2 = 0. Thus,
   y₁ = 0
   and
   y₂³ + 2 = 0
   y₂³ = - 2
   y₂ = √-2
   This value is approximately - 1.26. The corresponding x-values for these y-values are obtained by substituting the values found for y in the second equation.
   x₁ - y₁² = 0
   x₁ - 0² = 0
   x₁ = 0
   and
   x₂ - y₂² = 0
   x₂ - (√-2)² = 0
   x₂ = -2^2/3
   This value is approximately 1.587. Hence, the intercept points of the two graphs that belong to the equations of the original system, are A(0, 0) and B(1.587, - 1.26), as shown in the figure below.

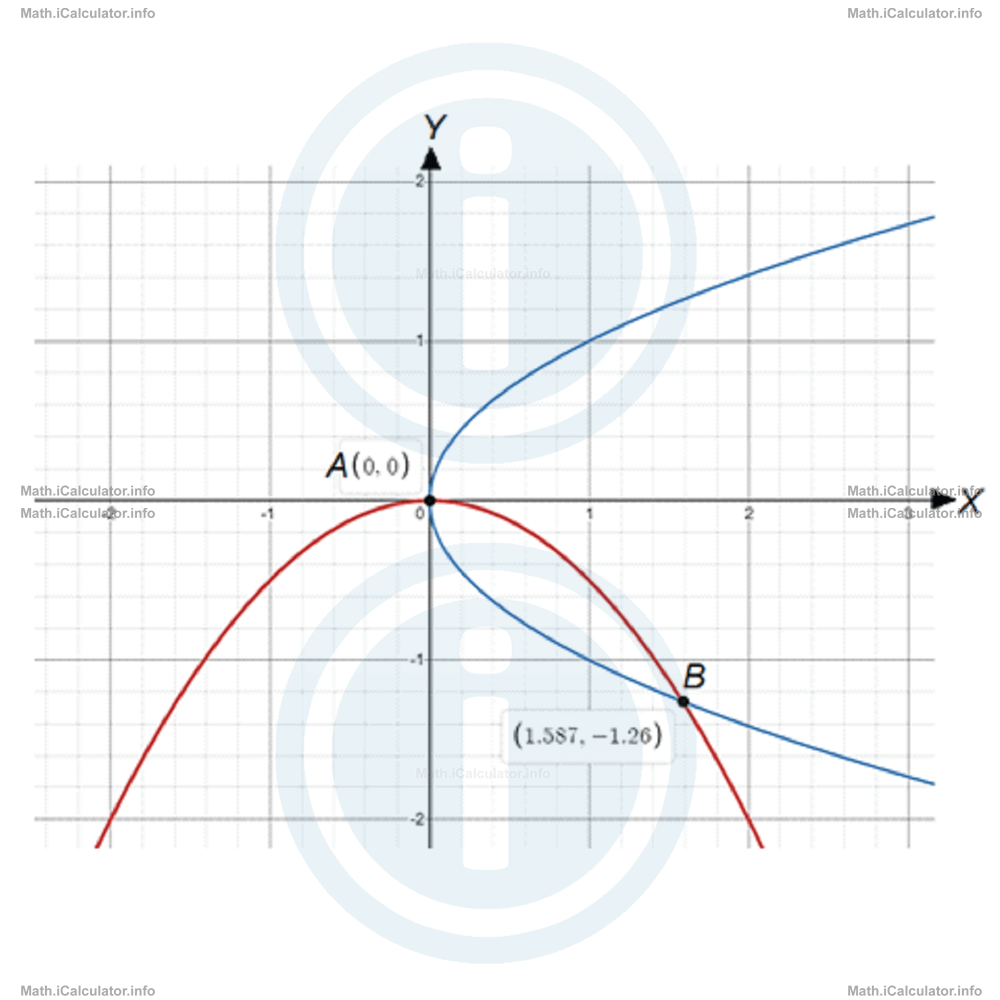
More Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation Lessons and Learning Resources

Whats next?

Enjoy the "Systems of Equations with One Linear and One Quadratic Equation" math lesson? People who liked the "Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation lesson found the following resources useful:

1. Quadratic Systems Feedback. Helps other - Leave a rating for this quadratic systems (see below)
2. Equations Math tutorial: Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation. Read the Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation math tutorial and build your math knowledge of Equations
3. Equations Video tutorial: Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation. Watch or listen to the Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation video tutorial, a useful way to help you revise when travelling to and from school/college
4. Equations Revision Notes: Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation. Print the notes so you can revise the key points covered in the math tutorial for Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation
5. Equations Practice Questions: Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation. Test and improve your knowledge of Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation with example questins and answers
6. Check your calculations for Equations questions with our excellent Equations calculators which contain full equations and calculations clearly displayed line by line. See the Equations Calculators by iCalculator™ below.
7. Continuing learning equations - read our next math tutorial: Variables, Coefficients and Constants. First Order Equations with One Variable

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Relationship between Equations in Linear Systems. Systems of Equations with One Linear and One Quadratic Equation" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Equations Calculators by iCalculator™

• Completing The Square In Quadratics Calculator
• First Order Equations With One Variable Calculator
• First Order Equations With Two Variables Calculator
• Solving Quadratics Through The Quadratic Formula
• Solving Systems Of Linear Equations With The Substituting Method Calculator
• Solving Systems With One Linear And One Quadratic Equation Calculator