Math Lesson 3.5.2 - The Meaning of Decimals. Converting Fractions into Decimals without a Calculator

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Math lesson on The Meaning of Decimals. Converting Fractions into Decimals without a Calculator, this is the second lesson of our suite of math lessons covering the topic of Converting Fractions to Decimals and Vice-versa, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.

The Meaning of Decimals. Converting Fractions into Decimals without a Calculator

Decimals are an alternative representation of decimal mixed numbers. They are made of two parts: the left part which shows the whole part of the corresponding decimal mixed number and the right part which shows the numerator of the fractional part of the corresponding decimal mixed number. A dot known as decimal point separates the whole and decimal part of such numbers.

In other words, the decimal mixed number 3 7/10 is alternatively written as 3.7 where 3 shows the whole part of the corresponding mixed number and 7 the numerator of the fractional part of this number. In symbols, we write

and so on.

The number of zeroes in the denominator of the decimal mixed number determines the number of digits after the decimal point (we say "the number of decimal places"). Thus, if the denominator of the mixed number is 10, the corresponding decimal has one decimal place, if the denominator of the mixed number is 100, the corresponding decimal has two decimal places and so on.

Example 3

Express the following mixed numbers as decimals.

Solution 3

1. Since the denominator of this mixed number is 10, the corresponding decimal has one digit after the decimal point. Thus, we have
   15 9/10 = 15.9
2. It is impossible to write the denominator of this mixed number as 10 but we can write it as 100 by multiplying up and down by 2. As a result, the corresponding decimal will have two digits after the decimal place. Thus, we have
   7 29/50 = 7 (29 × 2)/(50 × 2) = 7 58/100 = 7.58
3. This time the denominator can neither be 10 nor 100 but only 1000. Hence, the corresponding decimal will have three decimal places. We have
   100 1/8 = 100 (1 × 125)/(8 × 125) = 100 125/1000 = 100.125

As for the other fractions that cannot turn into decimal fractions, we apply the normal division of their numerator and denominator using the division method explained in tutorial 1.3. In most cases, this division gives an infinite number of digits after the decimal place but if you look them carefully, you will detect a kind of recurrence, i.e. the pattern is repeated after a number of digits. For example, when written as decimal, the fraction 3/7 becomes

As you see, the recurring part highlighted in yellow is repeated an infinity number of times as this decimal has no end. When we are completing the division by using the method described in tutorial 1.3 and we notice the repetition of two digits, it is quite probable that the recurrence has already began to appear. Let's consider an example in this regard.

Example 4

Express the following fractions as decimals.

Solution 4

1. We have 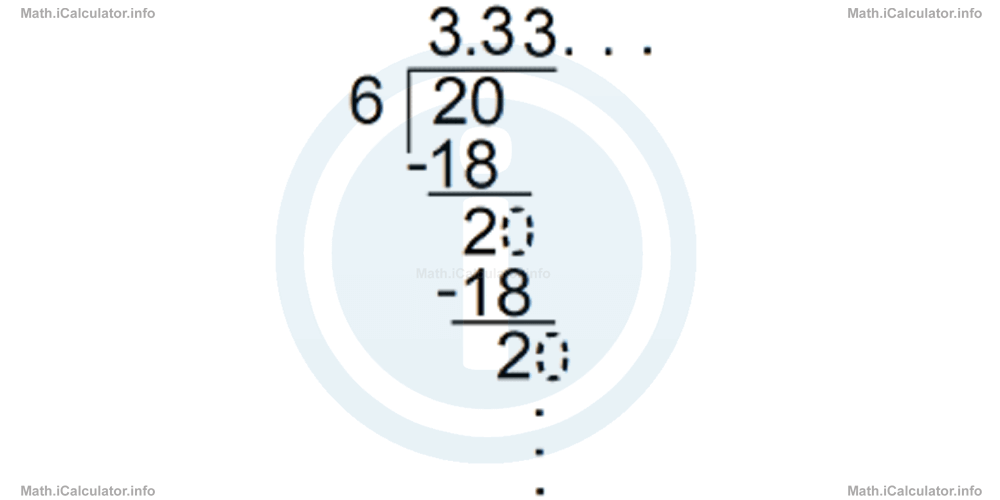Hence, the result is a recurrent decimal, 3.333333. which continues to infinity. We use a horizontal line above the recurring part to indicate that that part of the number is repeated continuously. Therefore, instead of writing 3.33333. we write 3.3 to indicate the recurrence.
2. We have 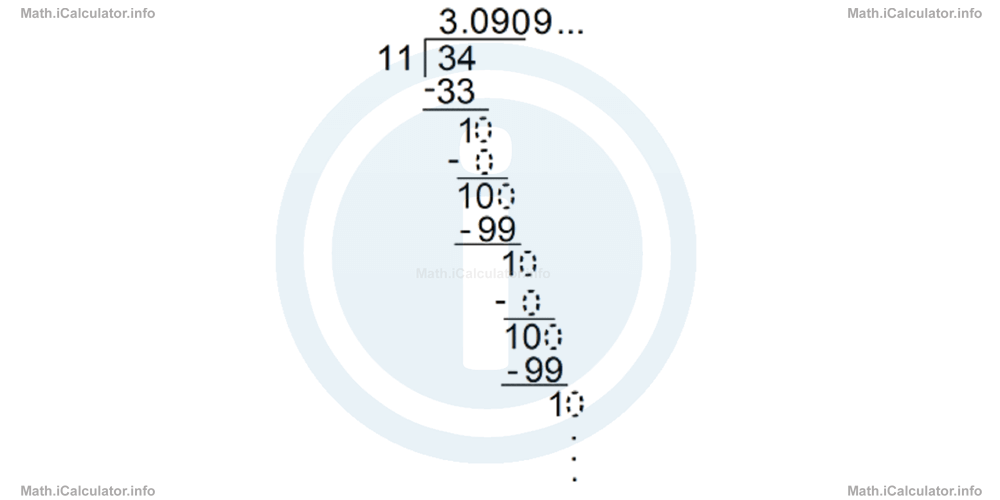Hence, the result is a recurrent decimal, 3.0909. which continues up to infinity. We use a horizontal line above the recurring part to indicate that that part of the number is repeated continuously. Therefore, instead of writing 3.0909. we write 3.09 to indicate the recurrence.

More Converting Fractions to Decimals and Vice-versa Lessons and Learning Resources

Whats next?

Enjoy the "The Meaning of Decimals. Converting Fractions into Decimals without a Calculator" math lesson? People who liked the "Converting Fractions to Decimals and Vice-versa lesson found the following resources useful:

1. Fraction To Decimal Feedback. Helps other - Leave a rating for this fraction to decimal (see below)
2. Fractions Math tutorial: Converting Fractions to Decimals and Vice-versa. Read the Converting Fractions to Decimals and Vice-versa math tutorial and build your math knowledge of Fractions
3. Fractions Video tutorial: Converting Fractions to Decimals and Vice-versa. Watch or listen to the Converting Fractions to Decimals and Vice-versa video tutorial, a useful way to help you revise when travelling to and from school/college
4. Fractions Revision Notes: Converting Fractions to Decimals and Vice-versa. Print the notes so you can revise the key points covered in the math tutorial for Converting Fractions to Decimals and Vice-versa
5. Fractions Practice Questions: Converting Fractions to Decimals and Vice-versa. Test and improve your knowledge of Converting Fractions to Decimals and Vice-versa with example questins and answers
6. Check your calculations for Fractions questions with our excellent Fractions calculators which contain full equations and calculations clearly displayed line by line. See the Fractions Calculators by iCalculator™ below.
7. Continuing learning fractions - read our next math tutorial: The Meaning of Fractions. Equivalent Fractions. Simplifying Fractions

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Math tutorial "Converting Fractions to Decimals and Vice-versa" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Fractions Calculators by iCalculator™

• Operations With Fractions Calculator
• Recurrent Decimals To Fraction Converter
• Writing Fractions In The Lowest Terms Calculator
• Equivalent Fractions Calculator
• Equivalent Fractions Table Calculator
• Fraction Calculator
• Fraction To Ratio Calculator
• Ratio To Fraction Calculator
• Simplifying Complex Fractions Calculator
• Ordering Fractions Calculator
• Which Fraction Is Bigger
• Which Fraction Or Percentage Is Bigger
• Which Ratio Or Fraction Is Bigger