Menu
Math Lesson 4.3.3 - Graph of Direct Proportion
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Math lesson on Graph of Direct Proportion, this is the third lesson of our suite of math lessons covering the topic of Proportion, you can find links to the other lessons within this tutorial and access additional Math learning resources below this lesson.
Graph of Direct Proportion
In ratio tutorial 4.1 we proved that ratios produce a linear graph. Since the direct proportion is obtained by two equal ratios, it is easy to conclude that the graph representing a direct proportion is a straight (sloped) line that starts from the origin (otherwise it is not a direct proportion), where the slope is determined by the simplest form of the ratio or of the unit rate.
Let's consider one such a graph to clarify this point.
The graph below is not an example of direct proportion because the ratios of position at the two given instants are not the same as the ratios of time. In other words, 320/110 is different from 20/10, as the first ratio gives 1.5 and the second gives 2. 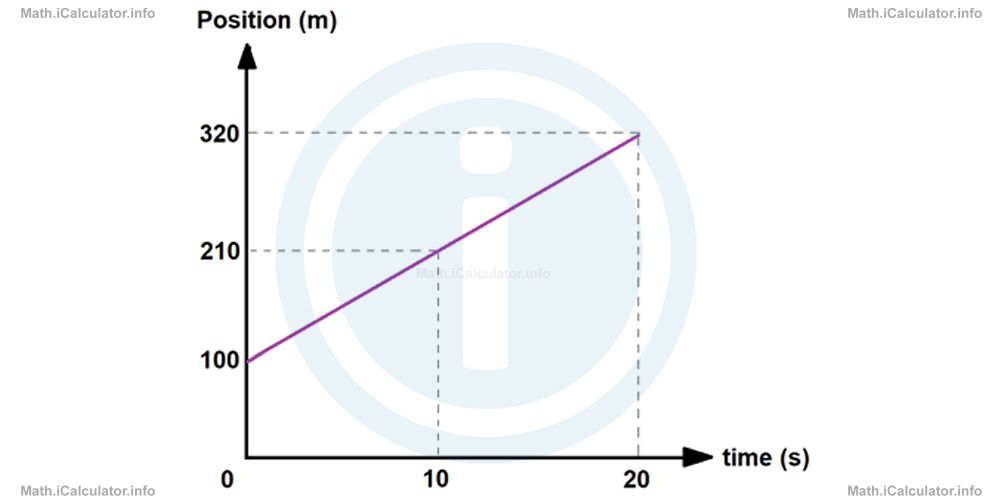
Therefore, the quantities involved in the above situation are not directly proportional. In simpler words, the graph must start from the origin in order to have a direct proportion, as shown below.
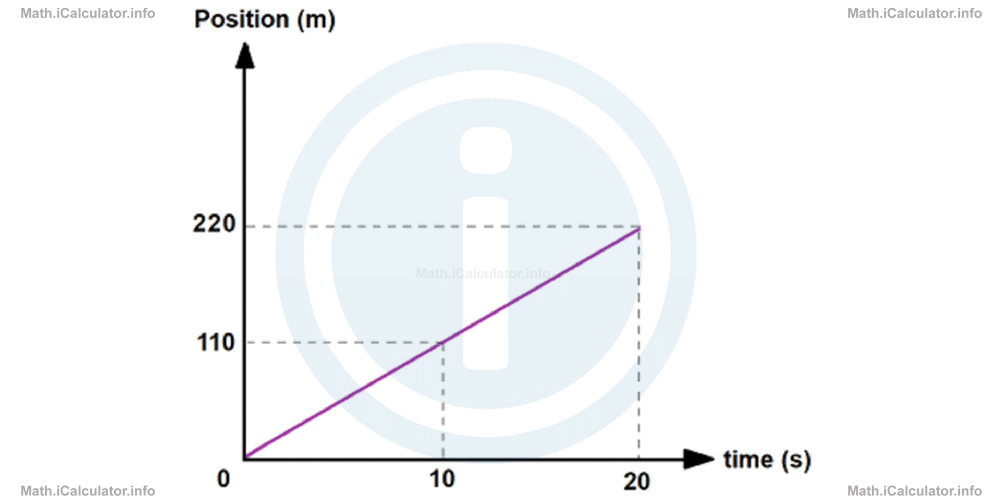
Here, both ratios are the same as 220/110= 20/10 = 2. Therefore, the quantities involved are directly proportional (or simply, proportional).
Remark! It is better to solve the situations with ratios, not with rates when dealing with proportions. In other words, it is better to divide two like quantities instead of the unlike ones.
Example 3
Which of the following situations involves a direct proportion?
- A car can travel 200 km with 12 L of fuel and other 300 km with 20 L of fuel.
- 5 kg of paint can paint 30 m2 wall while 12 kg paint can paint 72 m2 wall.
Solution 3
- We will check whether the ratios are equal by dividing the like quantities. We have 200 km distance/300 km distance and 12 L fuel/20 L fuelThe first fraction gives 2/3 while the second gives 3/5. Therefore, this situation does not involve a direct proportion.
- Again, we take the ratios. We have 5 kg paint/12 kg paint and 30 m2 wall/72 m2 wallThe first ratio is already in the simplest form, and the second ratio gives 5/12 too when written in the simplest terms. Therefore, the quantities involved are proportional.
More Proportion Lessons and Learning Resources
Whats next?
Enjoy the "Graph of Direct Proportion" math lesson? People who liked the "Proportion lesson found the following resources useful:
- Graph Feedback. Helps other - Leave a rating for this graph (see below)
- Ratio and Proportion Math tutorial: Proportion. Read the Proportion math tutorial and build your math knowledge of Ratio and Proportion
- Ratio and Proportion Video tutorial: Proportion. Watch or listen to the Proportion video tutorial, a useful way to help you revise when travelling to and from school/college
- Ratio and Proportion Revision Notes: Proportion. Print the notes so you can revise the key points covered in the math tutorial for Proportion
- Ratio and Proportion Practice Questions: Proportion. Test and improve your knowledge of Proportion with example questins and answers
- Check your calculations for Ratio and Proportion questions with our excellent Ratio and Proportion calculators which contain full equations and calculations clearly displayed line by line. See the Ratio and Proportion Calculators by iCalculator™ below.
- Continuing learning ratio and proportion - read our next math tutorial: Properties of Proportion. Geometric Mean
Help others Learning Math just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Math tutorial "Proportion" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.
Ratio and Proportion Calculators by iCalculator™
- Geometric Mean Calculator
- Joint Variation Calculator
- Ratio Calculator
- Ratio Solver
- Ratio Addition Calculator
- Ratio Subtraction Calculator
- Ratio Division Calculator
- Ratio Multiplication Calculator
- Relative Ratios Calculator
- Ratio Comparison Calculator
- Visual Ratio Calculator
- Ratio Finder
- Equivalent Ratios Calculator
- Equivalent Ratio Table Calculator
- Aspect Ratio Calculator
- Divide Ratio Calculator
- Ratio Divider Calculator
- Ratio Simplifier Calculator
- Golden Ratio Calculator
- 3 Ratio Calculator
- Sharing Ratio Calculator
- Equal Share Verse Ratio Share Calculator
- Values To Ratio Calculator
- Ratio Table Calculator
- Ratio Table
- Decimal Ratio Table Calculator
- Ratio Table Creator
- Ratio Converter
- Percentage To Ratio Calculator
- Ratio To Percentage Calculator
- Ratio To Fraction Calculator
- Fraction To Ratio Calculator
- Ratio To Decimal Calculator
- Decimal To Ratio Calculator
- Values To Ratio Calculator
- Which Ratio Or Fraction Is Bigger
- Which Ratio Or Percentage Is Bigger
- Which Ratio Is Bigger