You are here:
  1. / iCalculator
  2. / Ratio And Proportion
  3. / Rates And Ratios
  4. / Practice Questions

Menu

Rates. Applications of Ratios and Rates in Practice

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 1 Votes ]

The following math revision questions are provided in support of the math tutorial on Rates. Applications of Ratios and Rates in Practice. In addition to this tutorial, we also provide revision notes, a video tutorial, revision questions on this page (which allow you to check your understanding of the topic) and calculators which provide full, step by step calculations for each of the formula in the Rates. Applications of Ratios and Rates in Practice tutorials. The Rates. Applications of Ratios and Rates in Practice calculators are particularly useful for ensuring your step-by-step calculations are correct as well as ensuring your final result is accurate.

Not sure on some or part of the Rates. Applications of Ratios and Rates in Practice questions? Review the tutorials and learning material for Rates. Applications of Ratios and Rates in Practice

Ratio and Proportion Learning Material
Tutorial IDTitleTutorialVideo
Tutorial		Revision
Notes		Revision
Questions
4.2Rates. Applications of Ratios and Rates in Practice

Rates. Applications of Ratios and Rates in Practice Revision Questions

1. . An object moves in a straight line from position X1 = 2 m to another position X2 = 17 m during 3 seconds. What is the rate of position change?

  1. 19/3 m/s
  2. 17/3 m/s
  3. 5 m/s
  4. 3 m/s

Correct Answer: C

2. . A heart rate monitor gives the value 78. This means the heart of the patient beats.

  1. 78 times in total during the measurement process
  2. 78 times per minute
  3. 78 times per second
  4. Once in every 78 seconds

Correct Answer: B

3. . The price of an item dropped from $378 to $333 in three years. What was the annual rate of price drop?

  1. $15/year
  2. $111/year
  3. $126/year
  4. $45/year

Correct Answer: A

4. . The annual growth rate of a plant is 0.6 m/year. What is the actual height of the plant if its weight 4 years ago was 4.1 m?

  1. 4.7 m
  2. 1.5 m
  3. 6.7 m
  4. 6.5 m

Correct Answer: D

5. . What is the actual capital of a customer deposited in a bank if he will have $52,000 in total after two years? The annual interest rates of the bank are 2%.

  1. $48,000
  2. $50,000
  3. $51,000
  4. $54,000

Correct Answer: B

6. . A factory has 125 workers and they can produce 500 pairs of shoes in a day. What is the associated rate of shows/worker daily rate?

  1. 0.25
  2. 4
  3. 0.2
  4. 5

Correct Answer: A

7. . One of the quantities (the smallest) forming a golden ratio is 20. What is the value of the other (the biggest) quantity rounded to the nearest hundredth?

  1. 32
  2. 32.4
  3. 12.5
  4. 20

Correct Answer: B

8. . What is the rate of position change in the graph below?

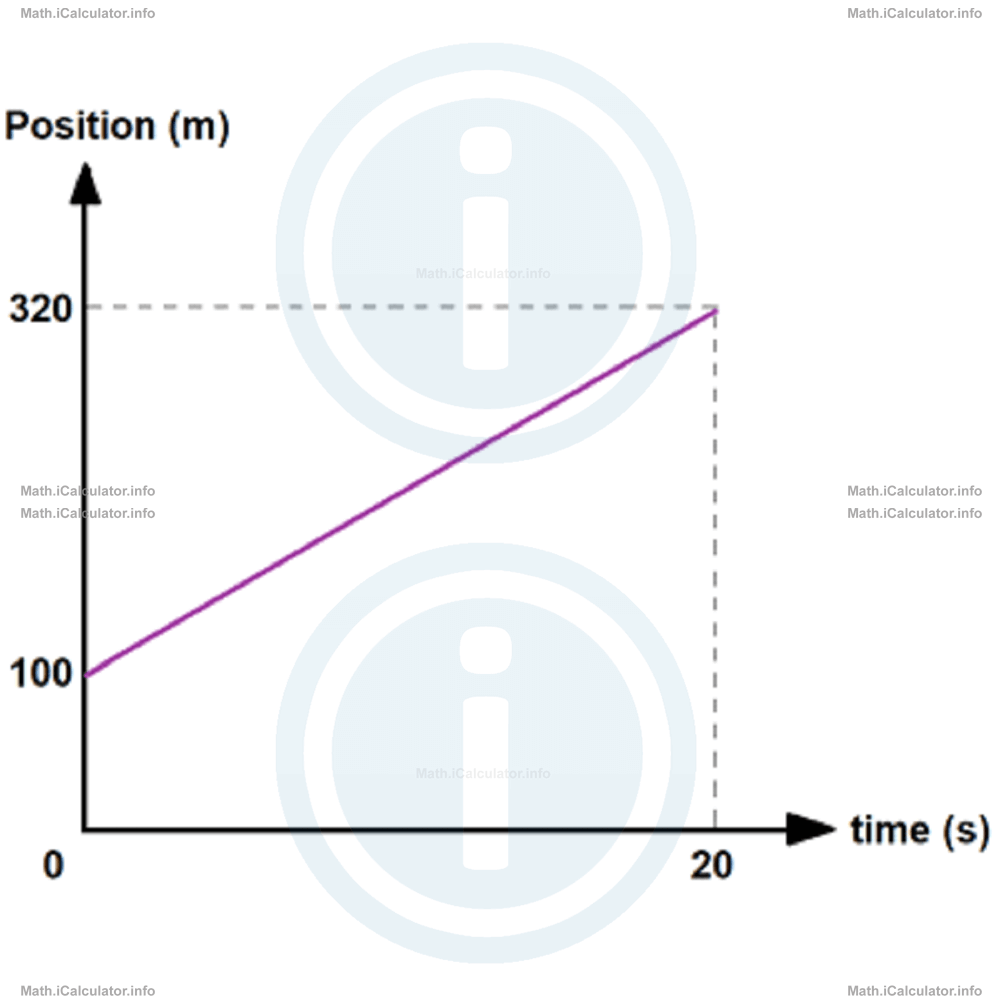
Math Tutorials: Rates. Applications of Ratios and Rates in Practice Example
  1. 220 m/s
  2. 16 m/s
  3. 11 m/s
  4. 5 m/s

Correct Answer: C

9. . A painting is 55 cm long and Y cm wide. Its dimension form a golden ratio with each other. What is the width of the painting? (Width is shorter)

  1. 86 cm
  2. 64 cm
  3. 50 cm
  4. 34 cm

Correct Answer: D

10. . 24 L of water flow in a minute through an open tap. What is the flow rate in litres per second?

  1. 40 L/s
  2. 4 L/s
  3. 2.5 L/s
  4. 0.4 L/s

Correct Answer: D

Whats next?

Enjoy the "Rates. Applications of Ratios and Rates in Practice" practice questions? People who liked the "Rates. Applications of Ratios and Rates in Practice" practice questions found the following resources useful:

  1. Practice Questions Feedback. Helps other - Leave a rating for this practice questions (see below)
  2. Ratio and Proportion Math tutorial: Rates. Applications of Ratios and Rates in Practice. Read the Rates. Applications of Ratios and Rates in Practice math tutorial and build your math knowledge of Ratio and Proportion
  3. Ratio and Proportion Video tutorial: Rates. Applications of Ratios and Rates in Practice. Watch or listen to the Rates. Applications of Ratios and Rates in Practice video tutorial, a useful way to help you revise when travelling to and from school/college
  4. Ratio and Proportion Revision Notes: Rates. Applications of Ratios and Rates in Practice. Print the notes so you can revise the key points covered in the math tutorial for Rates. Applications of Ratios and Rates in Practice
  5. Check your calculations for Ratio and Proportion questions with our excellent Ratio and Proportion calculators which contain full equations and calculations clearly displayed line by line. See the Ratio and Proportion Calculators by iCalculator™ below.
  6. Continuing learning ratio and proportion - read our next math tutorial: Proportion

Help others Learning Math just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 1 Votes ]

We hope you found this Math tutorial "Rates. Applications of Ratios and Rates in Practice" useful. If you did it would be great if you could spare the time to rate this math tutorial (simply click on the number of stars that match your assessment of this math learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.

Ratio and Proportion Calculators by iCalculator™

© iCalculator™ 2009 - 2024 | Math Calculators | Privacy Policy | Terms of Use | Contact